I love learning. But since, I graduated from UMich, I have not had any structured, consistent forms of learning in my life. That is until about last week, when I decided that I wanted to learn big-boy calculus, i.e., analysis. My good friend and Differential Equations professor from UMich, Dr. Pat Boland, was kind enough to share a link to “Baby Rudin” with me years ago, and only now have I found the motivation to dive into it.

I minored in Math during school, I took introductory linear algebra, stats and probability, numerical methods (supremely cool class), multivariable calculus, and differential equations, not to mention the various calculus involved in my chemical engineering classes. However, I avoided pure-maths like the plague during school – “I’m an engineer, anything but applied maths is a waste of time,” I thought. Boy was I not totally wrong. But, math can be learned for the sake of enjoying math, which is as worthwhile a reason as any.

Proofs are hard. The few times I encountered proofs in the classes listed above, they didn’t really make sense to me. The statements made and the steps taken by my math-major colleagues while writing proofs made little sense to me – either huge leaps in understanding that left me confused, or unbearably simple statements that seemed entirely unnecessary. But yesterday, I had my first breakthrough where some proofs made sense. That is what I would like to share on my blog today: one of the propositions about ordered fields I proved yesterday (yes fields are an algebraic construct, not something within the realm of analysis. But in construction of the real and complex fields, twas necessary to be defined).

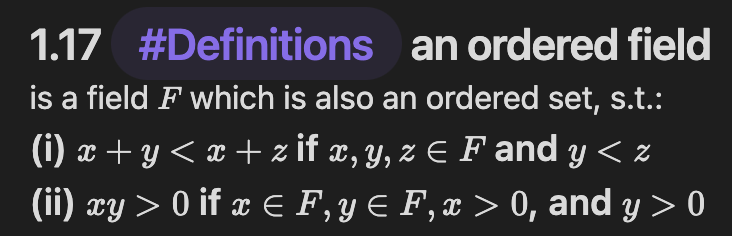
It was previously established what an ordered set is (a group of numbers upon which the “>”, “<“, and “=” comparisons hold), and what a field is (a set in which the axioms of addition and multiplication hold). The marriage of these two concepts into an ordered field is a slight challege, and involved proving the following propositions:

1.18(c) is my personal favorite amongst the bunch, because it is a rigorous statement that essentially says “when you multiply a negative across an inquality, the inequality is flipped (> becomes < and vice versa).” The earliest time I remember this statement was during like 7th grade, so well over a decade ago. And yet, proving 1.18(c) was not simple:

Though extremely ugly, and not exactly the way Rudin proved proposition 1.18(c), this (I’m pretty sure) is correct, and all of my own design! Essentially, I applied previously proven propositions or established axioms to validate each step, manipulating the left and right hand sides of the intial statements until we arrive at the equation we aimed to prove:

1. The initial proposition states that if “x < 0” (x is negative), and “y < z”, then “xy > xz”.
2. Step 1 takes the initial statement “y < z” and uses the definition of ordering to show that “y-z” is a negative number, i.e., the quantity is < 0.
3. Next, we add the term of equal and opposite magnitude, “-(y – z)” to each side
4. Since “x < 0”, I applied a previously proven statement to say that “-x > 0”, i.e., negative x is positive. Moreover, two positive numbers multiplied together result in another positive number. I used these two statements to assert that (-x)[-(y-z)] > 0 (is positive).
5. I then distribute the (-x) to the terms in -(y-z), and then subtract the term (-x)[-(-z)] from both sides, to get “xy > -[(-x)z]”. Again, a two negatives become a positive, and thus -[(-x)z] becomes xz, and so the final equation is “xy > xz” which is exactly what we wanted to prove.

Though this is an extremely simple proof (literally on page 8 of the 300+ page textbook), I am proud of myself for doing it on my own and understanding what I’ve learned previously (in the first 7 pages…) enough to correctly prove these new statements. It felt like solving a puzzle – I had an assortment of different pieces that d collected thus far that I needed to arrange in a new pattern to form a new puzzle piece!

This was very rewarding for me and motivates me to continue learning and studying analysis! My primary goal with respect to studying mathematics is getting into differential geometry so that I can get deeper into the fundamental building blocks of machine learning and AI, but real and complex analysis is somewhat perpendicular to that goal. Functional analysis may be slightly more conducive to getting into machine learning, but real/complex analysis is more useful in physics and control theory than AI (as the fields stand today).

However, I still think analysis is useful to learn; I am filling in the gaps and reinforcing the foundational layers of mathematics in my mind, as well as practing the thought patterns necessary to rigorously understand the concepts that I will encounter on this journey. I can almost feel my brain becoming more plastic as I force myself to think in ways unfamiliar to me in order to solve these problems!

Stay tuned for more!